Summary generation is one of the most common applications of large language models (LLMs). It delivers value by compressing lengthy documents or dense, technical research papers into accessible narratives. However, trust in these summaries remains low. The challenge lies not only in the subjective judgments about adequacy but also in the frequent failure of models to preserve critical information from their sources when generating the summaries.
Evaluating completeness is difficult because it depends on subjective interpretations of what should be included. A more tractable approach is to evaluate incompleteness - generally defined as the failure of a summary to retain salient information from its source. Incompleteness can take many forms: omissions, overgeneralization, partial inclusion of key facts, paraphrasing losses or outright distortions. Empirical evidence shows that LLM-generated summaries often exhibit such gaps. But the sunny side is that these forms of incompleteness can be identified and assessed objectively.
There are many existing models. The model’s ability to summarize can be evaluated using those. Table 1 shows the most popular models with their key characteristics.
| Method | Supervision | Granularity | Cost |
| ROUGE/METEOR | None | Global | Low |
| BERTScore/MoverScore | None | Global | Low |
| QuestEval / UniEval/QAGS/FactCC | Yes | Segment | High |
| FineSurE/G-Eval(LLM-as-a-Judge) | Yes | Segment/Global | Very High |
| Ours | None | Segment | Low |
(Table 1)
Existing evaluation methods generally fall into two camps. The first relies on global similarity metrics, which can detect broad correlations with incompleteness but fail to pinpoint where content is missing. The second group uses supervised QA, natural language inference (NLI), or LLM-as-judge methods. These approaches provide more detailed adequacy signals but come with high costs in data, annotation and ongoing maintenance.
We propose a novel framework that bridges this gap with an unsupervised, one-class classification-inspired (OCC) method. Instead of relying on paired labels or large annotated datasets, OCC focuses on learning the characteristics of a single target class. Applied to summarization, this translates into identifying incompleteness at the segment level. To achieve this, we leverage Lie algebra–based transformations, which allow us to capture subtle variations in semantic flow. The result is a set of interpretable, flow-based signals that highlight where key information may have been omitted, without the overhead of supervision.
We propose a Lie algebra–driven semantic flow framework to identify incompleteness in summaries. In this view, summarization is modeled as a geometric transformation that maps context embeddings into a summary space. Each part of the source text creates a flow vector that shows how much it contributes to the final summary. Incompleteness arises when some segments display unusually low flow magnitudes within a reduced semantic manifold. By formulating the detection as a one-class classification problem, our approach provides a unique balance between theoretical rigor and practical utility in evaluating summaries.
This design produces interpretable, segment-level signals that can be used in human-in-the-loop reviews, guided by a dynamic, mean-scaled thresholding mechanism. The method is unsupervised and delivers an average 30% improvement in F1 over contemporary approaches. The strength of the framework lies in its ability to detect a diverse spectrum of incompleteness — from omissions and paraphrasing losses to partial inclusions.
We call this the Lie algebra–based semantic flow framework for incompleteness detection. Alongside empirical gains, it comes with a theoretical foundation: proving rotation invariance, bounded flow behavior and a severity–coverage Pareto frontier that explains why moderate thresholds maximize performance.
A Lie algebra–based semantic flow framework for incompleteness detection, with a theoretical analysis covering rotation invariance, bounded flows and the severity–coverage Pareto frontier. It has shown 30% improvement over the existing methods on F1 improvements. Qualitative analyses showed that this method identifies omissions, generalizations and paraphrasing losses that similarity-based metrics often under-detect, providing interpretable and actionable evaluation signals.
Lie group and Lie algebra
Before going into more detail, let’s first explore the fundamental concepts behind the framework.
A Lie group is the set of all possible “transformations” of a certain type — like all rotations in n-dimensional space. For example, the elements of the group for the car’s steering wheel can be 90°, 180°, or 360° rotations. The 3600 rotation is actually a do nothing element or the identity element and it’s equivalent to a do-nothing motion and is present in all the symmetry groups.
A Lie group is also a smooth manifold. That means it has group operations (identity, associativity and inverse) like usual symmetry groups and continuous and differentiable structures like manifolds. It’s a mathematical way of describing smooth movements like rotation, reflection and translation.
The algebra helps describe the interaction between the tangent space and the identity element. Or, to put it another way, all the directions of the tiny nudges from the initial point of rotation. It zooms in on local behavior around identity transformations. Each element is a skew-symmetric matrix which describes the direction of the moment called the infinitesimal generator of motion.
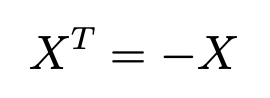
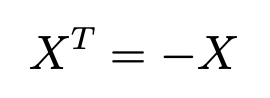
If we know the tiny push X, then exponentiating it describes the complete transformation, in this case, the rotation R:
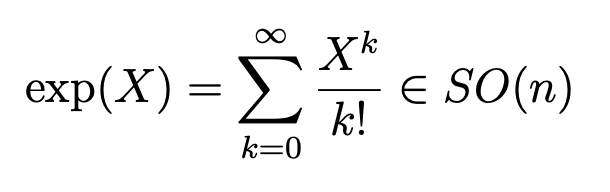
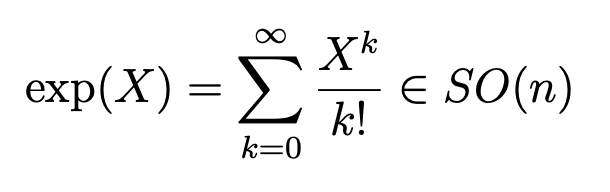
Skew-symmetric matrices are special mathematical objects that capture pure spinning behavior. They’re what happens when you say, “I want to turn, but not stretch or flip.” A skew-symmetric matrix represents a pure rotation around the origin. Applying it to a vector gives a direction of instantaneous motion along the tangent to the rotation.
On the other hand, if we know the rotation, to find which tiny push generates it we can use the matrix logarithm. This maps the full rotation back down to the Lie algebra, which allows us to measure small directional changes.
It’s possible to use cosine similarity here — the standard tool used by ML engineers — instead of Lie algebra; however, cosine similarity only offers a single score to describe the closeness of the two sentences. If we want to know how each sentence has been changed during summarization, that can be achieved only using Lie algebra. Linear algebra helps to detect how each sentence has moved — how much it gets used, reworded or ignored.
Let’s now dive into the core framework.
The core framework algorithm
The core framework algorithm helps us quantify how much each source sentence rotates into the summary space. The summary can be imagined as the rearranged version of the source sentences. You can imagine this rearrangement as a rotation — it’s like turning a 3D object (like a cube or a cylinder) as it preserves the meaning but changes the arrangement.
The algorithm can be broken down into multiple steps, like this:
| Step. | Description |
| 1 | Embed all segments from the source and summary using a language model
Context C = { c₁...cₙ} and summary R = {r₁...rₙ}
\( c_i = f_{\text{LM}}(c_i), \quad r_j = f_{\text{LM}}(r_j) \)
This yields embeddings:
C \(\in\) R ⁿˣᵈ and R \(\in\) Rᵐˣᵈ
|
| 2 | Apply principal component analysis (PCA) to reduce to a k-dimensional semantic space Concatenated embeddings Cₘ = C·P[:,: k], Rₘ = R·P[:,: k] There are advantages — this projection on the k-dimensional manifold creates:
[PCA is a method to summarize “high-dimensional data” by finding “new axes” (principal components) that capture the largest “patterns of variation”, allowing to “reduce” complexity while keeping most of the information.] |
| 3 | Align embeddings by finding the best orthogonal transformation (a rotation in this case) that brings them close to their average — using SVD in the same way as the classic orthogonal Procrustes problem.
Estimate optimal transformation T from source to summary.
Average summary embedding:
\( \bar{r} = \frac{1}{m} \sum_{j=1}^{m} r_j \)
So,
\( T = \arg\min_T \left\| C_M T - \bar{r} \cdot \mathbf{1}^\top \right\|_F^2 \).
\( T = U \Sigma V^\top, \quad T_{\text{orth}} = U V^\top. \)
This is exactly the orthogonal Procrustes problem, a well-known method for aligning vector spaces. So our approach is built on a rigorous, widely used mathematical framework.
[The Singular Value Decomposition (SVD) is a way to break any matrix A into three simpler pieces:
Vᵀ: rotates the input space into a nice orientation.
Σ: stretches/squeezes along the coordinate axes (by the singular values).
U: rotates the result to the output space.
So any linear transformation is basically: rotate → stretch → rotate.]
|
| 4 | Map Tₒᵣₜₕ to its Lie algebra using matrix logarithm
$$
|
| 5 | Compute the semantic flow vector for each source segment cᵢ
vᵢ - cᵢXᵀ, mᵢ=||vᵢ||₂
cᵢ - segment embeddings
We have computed the transformation X. Now we apply X to each segment to get the semantic flow vector. Then we take its norm, that is its length. vᵢ tells us how much the segment points into the aligned summary space. The norm mᵢ (length of this vector) tells us how strongly that segment contributes to the overall summary embedding.
If mᵢ is:
Using the Lie algebra turns a global, uniform rotation into a set of local “micro-rotations,” so we can detect which segments are weakly represented — if we didn’t do this, all segments would look the same and any omissions would be invisible.
|
| 6 | Determine the threshold of the magnitude mᵢ using the mean-scaled rule.
\(\tau=\alpha.\frac{1}{n}\sum_{i=1}^{n}\) mᵢ,
M = {cᵢ \(\in C | mᵢ <\tau\) }
Where \(\alpha\) > 0 is a tunable parameter.
The \(\alpha\) It sets the sensitivity for the method. A high “\(\alpha\) ” means flagging of the most ignored sentences. A low “\(\alpha\) ” means inclusion of mildly underrepresented ones. This parameter is tunable.
Segments with mi < τ are flagged as underrepresented (missing content) and the corresponding summary is marked as incomplete. |
Peculiarities of the framework
This is a geometrical framework. As the geometry doesn’t depend on the specific language, the geometrical framework can be used for models that support any language.
The PCA removes the messy parts of the sentence embeddings and keeps the useful meaning signals.
Each component of the framework is differentiable. This means we can plug it into training loops, such as a loss function that encourages completeness.
This framework can’t detect hallucinations; it can only tell what’s missing from the summary.
There are other methods to model semantic flow such as optimal transport method, attention encoder method and gated attention GNNs. However, this framework offers mathematical clarity and precision.
The framework works efficiently on large batches of documents equally well.
Datasets and benchmarks
Two benchmarks were used to test the framework. UniSumEval contains 225 contexts from diverse domains with incomplete summaries from small language models (SLMs). SIGHT, meanwhile, comprises 500 dense academic lecture transcripts, each summarized with GPT-4. Together they enabled evaluations across lightweight SLM outputs and state-of-the-art LLM outputs, capturing a broad spectrum of incompleteness.
The framework used four sentence encoders: all-MiniLM-L6-v2, all-mpnet-base-v2, bge-base-en-v1.5 and gte-base. We fixed k = 50 for all experiments, balancing computational efficiency with semantic fidelity. We formulate the problem as a one-class classification task to detect incompleteness. For evaluation, we compared our method against widely used ROUGE-1, BERTScore, InfoLM and G-Eval methods.
Qualitative examples of flagged incompleteness


Conclusion
We attempted to tackle the problem of evaluating incompleteness in machine-generated summaries, where traditional overlap and embedding-based metrics often fall short. We’ve proposed a Lie algebra–driven semantic flow framework that models summarization as a geometric transformation in embedding space, providing unsupervised, interpretable, segment-level signals.
On the selected benchmarks, our approach consistently outperformed ROUGE, BERTScore and InfoLM, achieving average absolute F1 gains of approximately +0.50. We demonstrated that coverage and severity serve as effective proxies for recall and precision and that their Pareto frontier explains F1 saturation at high α. Qualitative case studies further confirmed the framework’s ability to identify diverse types of incompleteness.
Future directions
Future work includes extending the framework to multilingual and context-adaptive embeddings and broadening its scope to jointly capture factuality and coherence.
Disclaimer: The statements and opinions expressed in this article are those of the author(s) and do not necessarily reflect the positions of Thoughtworks.


















