Uncertainty is intrinsic to machine learning and AI applications. During model training, uncertainty can be propagated into the model in many ways. They include noisy data, data that’s limited in describing full data variability (such as part of a huge dataset or data collected from an infinite stream of data), a model that is too large for a non-complex prediction task, which causes parts of it to be unnecessary, and even model training algorithms that don’t achieve the best model parameters. While these factors can be mitigated, they cannot be removed. Therefore, the ability to quantify a model's uncertainty is crucial for evaluating its reliability.
Uncertainty in a model refers to how unsure the model is about its output, also known as its prediction, for a given input. Uncertainty can be represented by the variability in the model’s prediction — in other words, the range and frequency of possible outputs for a given input. Another concept that is similar to uncertainty is confidence, which relates to the probability of a specific output, such as the output having a confidence of 60% for a particular class Y out of a number of classes. Overall, uncertainty is a more informative metric than confidence as it considers the full output distribution instead of specific output probabilities.
Two fundamental uncertainties
There are two fundamental types of uncertainty when dealing with AI models.
Statistical uncertainty: Sometimes called aleatoric or irreducible uncertainty, This is caused by the inherent randomness within data; while it’s hard to remove, it can be reduced by increasing the accuracy of the data measurement and collection methods.
Epistemic uncertainty: Also known as model uncertainty or reducible uncertainty, This is caused by gaps in data from outside the knowledge boundary of the model. Determining epistemic uncertainty can be challenging as large models use vast training data that can’t be completely curated. That makes it difficult to delimit the model’s knowledge boundaries. However, this uncertainty can be reduced by techniques such as data augmentation.
Besides statistical and epistemic uncertainty, there are others worth noting. These include uncertainty introduced by model assumptions, such as model size and model architecture that are not perfectly suited to the task at hand. Hence, uncertainty estimation helps us assess the overall reliability and robustness of the model. We can then understand potential errors associated with the model’s prediction and the risks should we adopt the predictions.
Uncertainty estimation is useful in domains like healthcare, space, finance and defense where it’s particularly important for decision-makers to make sound judgments. Finally, user trust is enhanced by quantifying uncertainty in predictions made by generative AI applications such as large language models (LLMs). An example would be to draw a knowledge boundary around the internal state of the LLM to mitigate potentially hallucinatory outputs.
Challenges to uncertainty estimation
The LLM ecosystem is diverse. LLM frameworks vary greatly by design, implementation, compute needs and usage; these factors invariably affect how the entire model’s uncertainty should be accurately quantified.
In the following table, we show a categorization of modern LLMs and their unique challenges to uncertainty estimation.
| Models | Challenges to Uncertainty Estimation |
| Open model | Open access to model weights, gradients and outputs such as intermediate outputs and logits. Comprehensive uncertainty estimation is possible with full model access. While the training data and training algorithm is useful for uncertainty estimation, they may not be released. Examples: Gemma and Llama models
|
| Transformers | Hugging Face provides a standardized interface to fine-tune, evaluate and deploy models starting from pre-trained models. The specificity to pre-implemented models makes uncertainty estimation more challenging to integrate. Examples: Hugging Face pre-trained models GPT-2, BERT, etc.
|
| Proprietary | Black box with no access to model internals. Ensemble modelling and uncertainty estimation are hard due to the API's limitations for probing the underlying models. Examples: GPT-3.5, GPT-4, DALL-E-3, etc.
|
| Multimodal | Multimodal inputs combine text, visual, audio or more modalities. This increases the complexity of uncertainty estimation due to varying modalities contributing differently to uncertainty. Additionally, the outputs can be multimodal as well, compounding the difficulty in uncertainty estimation. Examples: Gemini-2, GPT-4, Flamingo etc.
|
| Distributed | Designed for large-scale, parallelized model training and deployment. The specificity to distributed workloads can introduce variability to model states and intermediate outputs, thereby complicating uncertainty estimation. Examples: PyTorch Lightning, Fairscale, Horovod, etc.
|
Quantifying uncertainty in models
The uncertainty of the prediction in simple models, such as linear regression and classification models, are straightforward to quantify. On the other hand, deep neural networks (DNNs) are models with a large number of model weights. They have multi-dimensional, multi-layer and sophisticated architectures for learning from large datasets and achieving high performance on complex problems. As a result of this complexity, quantification of prediction uncertainty in DNNs is less tractable. Therefore, quantifying uncertainty for DNNs is more complicated and computationally intensive, so approximate methods need to be used instead.
To illustrate uncertainty estimation of a simple model, consider a linear regression model with uncertain parameters:


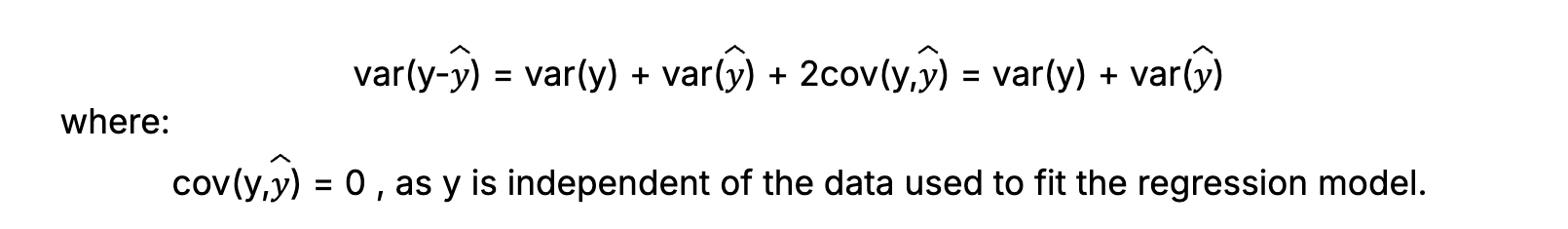
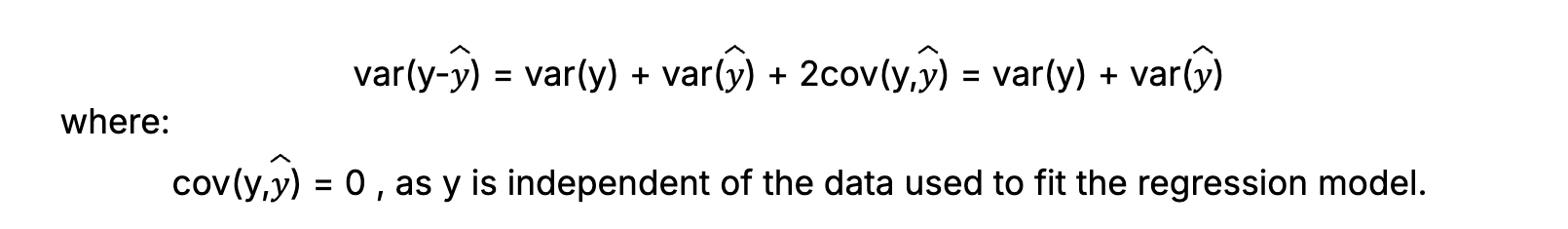
As shown above, the uncertainty derivation for a simple linear regression model is straightforward. On the other side of the spectrum, given a DNN with a complex architecture, diverse functions and a large number of layers and parameters, uncertainty compounds along the model and would be analytically intractable.
In this post, we will be walking through one practical and cost-effective method for uncertainty quantification: the dropout method.
Before jumping to the dropout method, let’s first familiarize ourselves with the Bayesian Neural Network.
Representing model uncertainty using Bayesian neural networks
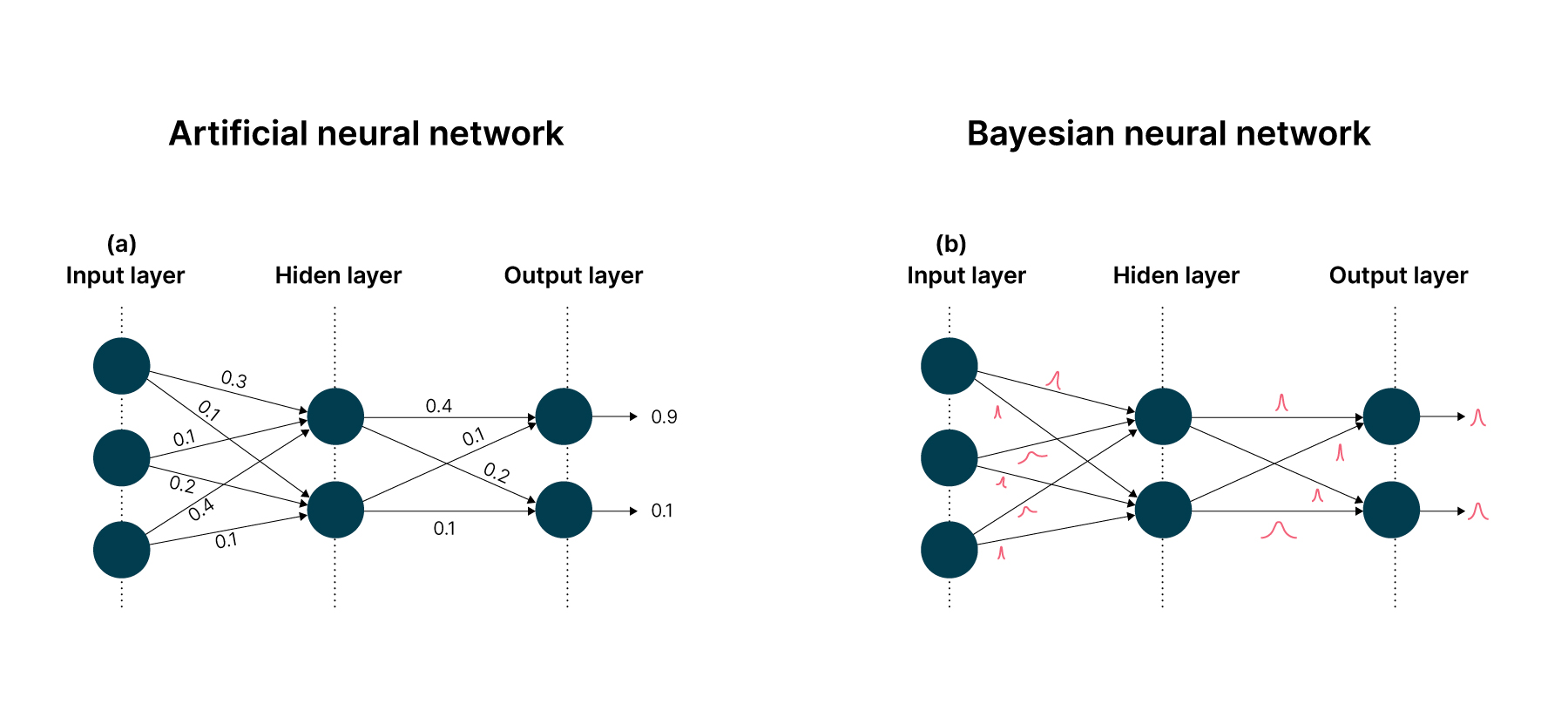
The synapses of ANN represent single valued weights and the synapses of BNN represent probabilistic distributions.
Many uncertainty estimation techniques are based on the mathematical foundations of Bayesian theory. Bayesian neural networks (BNNs) are networks where the weights W are treated as random variables and have a prior distribution p(W) instead of fixed values. This notion is a cornerstone of Bayesian inference; it reasons about the continual collection of data to update the range of weights and their likelihoods. This captures the uncertainty in weights, which in turn propagates to prediction uncertainty.
The Bayes’ theorem is as follows:


By marginalizing p(y|x,w) over the posterior p(w|D), the BNN considers all possible configurations of the network weights and their probabilities in making predictions. Although the Bayesian method is theoretically robust, as we see in this example, the computing costs needed by a BNN to directly compute the posterior distribution are high and prohibitive.
Fortunately, a technique that mitigates this challenge is the dropout method. It replaces the intractable problem of learning the original BNN’s posterior weight distributions with learning the weights of a representative neural network with dropping out applied to its weights.
The dropout method
Dropout refers to the random dropping out of weights of a neural network. The technique makes use of a simple distribution q(w) to approximate the true posterior distribution of the model weights p(W|X,Y). To achieve this, a distance between the two distributions, namely the Kullback-Leibler (KL) divergence, is minimized. Therefore, this method is equivalent to performing approximate variational inference. Now, connecting our chain of thoughts back to “Bayesian”, dropout can be interpreted as a variational Bayesian approximation technique.
In another view, dropout combines training multiple sub-networks of the original model and aggregates predictions from these sub-networks (each with randomly dropped weights from the original model) to approximate the overall model uncertainty; as such it can be regarded as an ensemble method. Also, dropout could drop neurons instead of weights to achieve a similar overall effect.
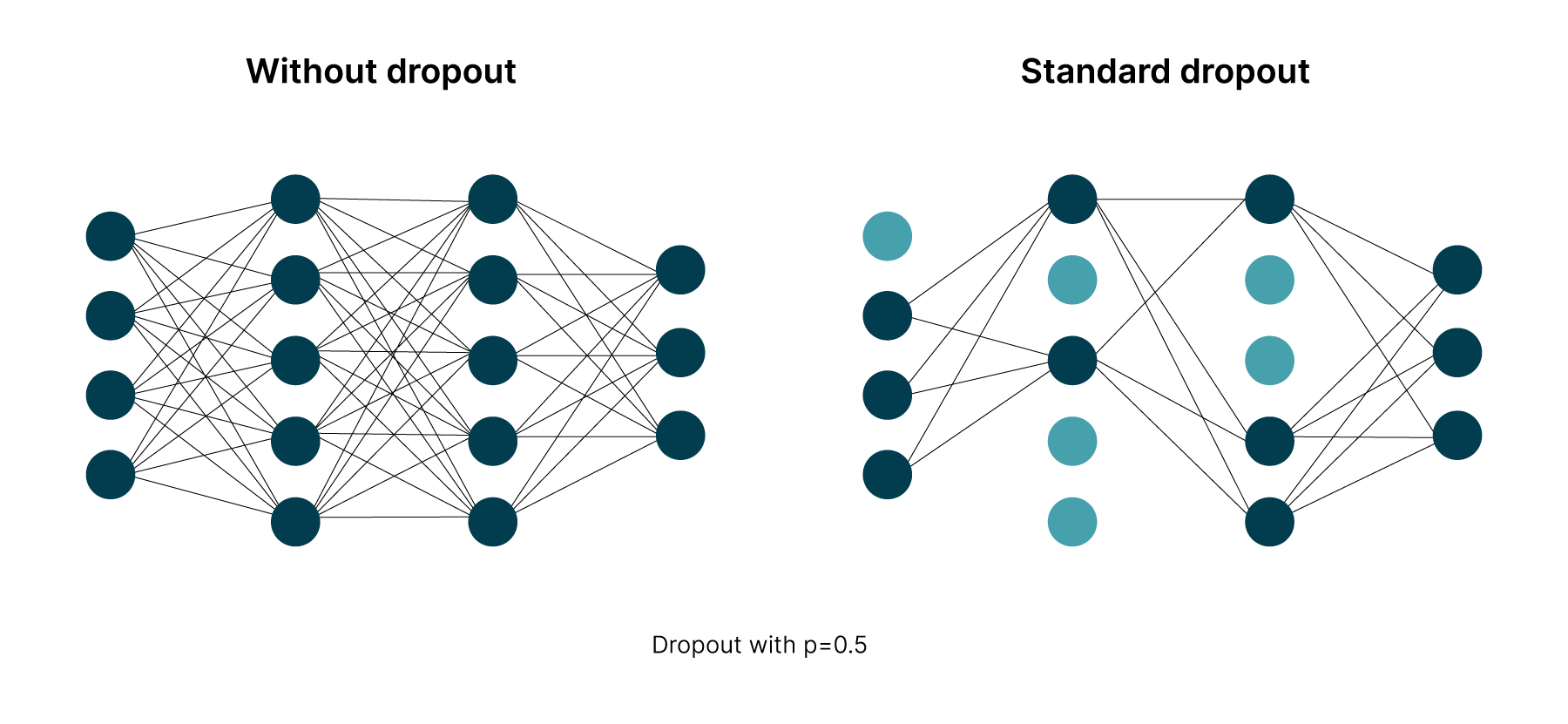
Practically, to implement dropout, neurons are randomly dropped with probability p in each training iteration that consists of a forward pass and a backward pass. Such neurons are deactivated, unable to contribute to the computations in the neural network for that training iteration, as shown by the network at the right of Figure 2. p is also known as the dropout rate. This behaviour is then repeated in all training iterations, achieving the overall effect of randomly thinning the original network during model training.
The comparison between a standard neural network and a dropout neural network is shown in Figure 2 and by the following equations.


Making inference with dropout


The overall equation represents two uncertainties: epistemic (due to insufficient data) and aleatoric (due to data randomness). It considers a distribution of predictions rather than a single deterministic output. The prediction made this way is more robust as it avoids over-relying on single point weight estimates and incorporates variability.
Estimating uncertainty
As we have seen earlier, T samples are collected in Equation three. Each represents a prediction given a sampled set of weights from the approximate posterior weight distributions. It turns out that the sample variance from the T samples can be computed to estimate how uncertain the model is about its prediction in the regression task. Briefly, for classification tasks the entropy of the mean probability vector (mean softmax outputs) can be used. This approach to estimating uncertainty is also known as Bayesian inference for uncertainty estimation.
Figure three shows two distributions of sampled predictions, followed with an explanation of how uncertainty estimation helps in decision making.
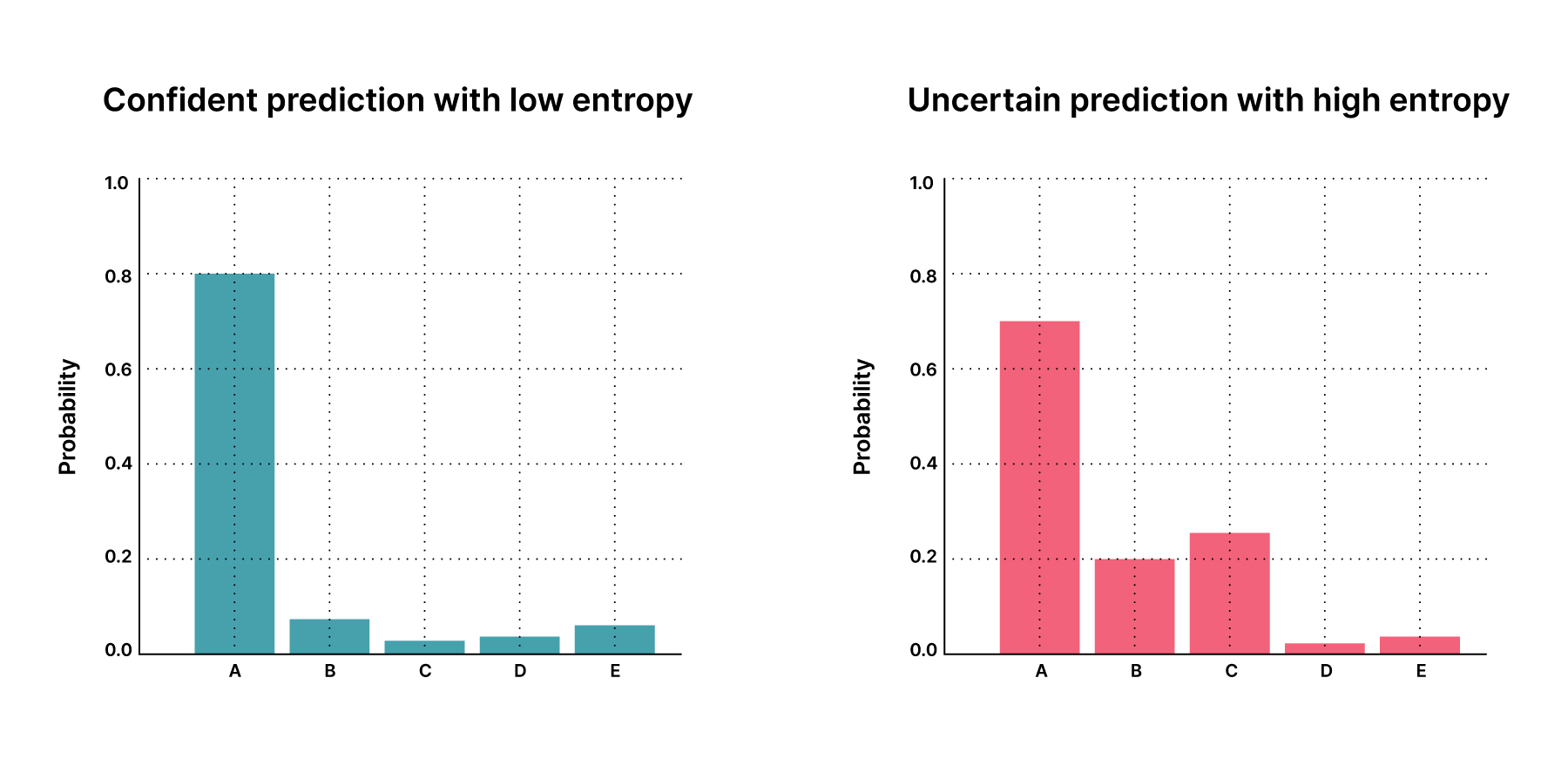
Confident prediction with low entropy (Figure 3: left chart in blue)
The mean probability distribution shows a sharp peak at class A as all sampled predictions agree strongly on class A (i.e. all softmax outputs peak highly at class A). Therefore the model is confident about its prediction and the entropy is low.
Uncertain prediction with high entropy (Figure 3: right chart in red)
The mean probability distribution shows significant spread over classes other than A. Even when the model assigns high overall probability to class A, the sampled predictions vary significantly (i.e. fluctuation of softmax outputs) and class A may not have been the class with the highest probability in all samples. Therefore the model is uncertain despite appearing quite confident on average, and the entropy is high.
The key insight is that when making judgments on predictions made by neural networks, it is generally inadequate to decide based on only the modal (highest probability) class. Rather, we should also consider the uncertainty associated with the prediction. While we could adopt a prediction having high probability and low uncertainty, it is crucial to perform a risk assessment on a prediction having high probability and high uncertainty.
Mitigating overfitting and co-adaptation
Large neural networks such as LLMs are trained on vast and complex data. During training, a large enough model could inadvertently learn the random noise inherent in the training data or even outliers. This results in overfitting. The model fails to generalize to unseen data, essentially memorizing the training examples (including the random noise and outliers) instead of adequately learning the underlying patterns and relationships within the data. As a result, it performs deceptively well on the training data but becomes unreliable in making inferences on new input data.
A large enough model could also be more susceptible to learning highly correlated behaviours amongst its weights, a phenomenon termed co-adaptation. When this happens, the weights do not capture independent but inter-related features and less useful narrow features. Consequently, when one neuron receives a low quality input leading to an inaccurate output, the co-adapted neurons, being highly-correlated, are likely to be impacted as well. Overall, this leads to a loss of generalization ability.
Dropout is one type of neural network regularization methods to reduce model overfit and co-adaptation. Dropout nullifies a random set of neurons in every training iteration, such randomness disrupts any memorization that could potentially take place in any neuron, thereby preventing model overfit to specific training examples. In addition, since a different network structure is realized from every dropout configuration sampled, the network distributes the learning of important features over a larger number of neurons. This redundancy enhances the model’s generalization to unseen data. Finally, as neurons are randomly dropped, co-adaptation between them is broken and they are encouraged to learn useful independent features, resulting in a more efficient model. The model also becomes more robust, not failing on specific feature interactions that do not hold well beyond the training data distribution.
Conclusion
In this post, we demonstrated how dropout can be a practical and more cost-effective method than BNNs for estimating the model’s prediction uncertainty given an input. In particular, the sample variance of a number of predictions from the given input can be computed to estimate how uncertain the model is about its regression task; while for classification tasks the entropy of the mean softmax outputs can be used. Finally, besides uncertainty estimation, dropout had been shown to be effective against overfitting, allowing the model to generalize better to unseen examples than models trained without dropout.
Disclaimer: The statements and opinions expressed in this article are those of the author(s) and do not necessarily reflect the positions of Thoughtworks.


















